About the music

Gaussian Curve is an ambient music trio composed by Young Marco, Gigi Masin and Jonny Nash. Gigi Masin is a long time ambient music producer and after the release of a compilation of his work, the two electronic music producers Young Marco and Jonny Nash started to work with him on the Gaussian Curve project and released Clouds, first album full of beauty.

About the science

A Gaussian function is a function with the form:

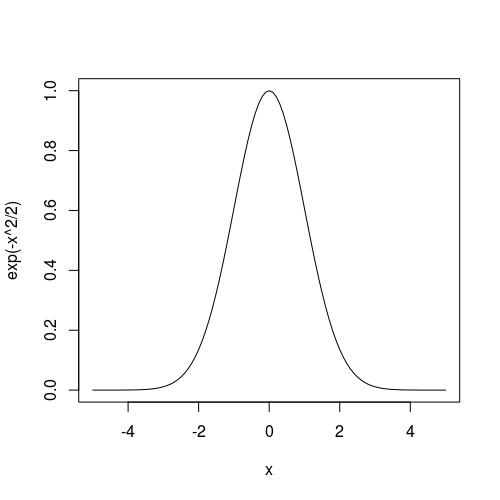
Thus for $a =1 $, $b = 0$ and $c = 1$ it gives the following well-known bell-curve.

Use in probabilities

The gaussian function is extremely important in probability theories. It’s a good way to estimate samples from nature, like the size of people of an age group, the salaries on a job market, etc … It is less and less likely to be of a certain value when we move from the average $\mu$. Randomly taking an 20 year old from a univeristy classroom, I have more chance to find a 1.80m tall than a 1.10m.

The parameters $b$ and $c$ from the equations are average and variance. Then we have to find $a$ so the function is a probability distribution. A (continuous) probability distribution (on $\mathbb{R}$) $f$ has the following property:

$$ \int_{-\infty}^\infty f(x)\,dx= 1 $$

Thus we find $a$ to normalize the distribution.

$$ f(x \; | \; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2} } \; e^{ -\frac{(x-\mu)^2}{2\sigma^2} } $$

The importance of the Gaussian Distribution comes from the Central Limit Theorem that says

Let $(X_1, …, X_n)$ be a sequence of independant and identically distributed random variables drawn from distributions of expected values $\mu$ and finite variance $\sigma^2$, then $$\sqrt{n}\left(\left(\frac{1}{n}\sum_{i=1}^n X_i\right) - \mu\right)\ \xrightarrow{d}\ N\left(0,\sigma^2\right)$$

Which means that the average of random noise controlled by $\sqrt{n}$ converge toward a Normal distribution. We see a lot of random noise in nature, so we also see a lot of gaussian distributions.

Other applications

The Gaussian function can be found in many other fields.

• In neural network, they are used as activation functions
• It’s a solution of the heat diffusion equation